Complexity Analysis of Brain Signals

Spontaneous brain activity is complex!

A defining but elusive feature of the human brain is its astonishing complexity. This complexity arises from the interaction of numerous neuronal circuits that operate over a wide range of temporal and spatial scales, enabling the brain to adapt to the constantly changing environment and to perform various amazing mental functions. In mentally ill patients, such adaptability is often impaired, leading to either ordered or random patterns of behavior. Quantification and classification of these abnormal human behaviors exhibited during mental illness is one of the major challenges of contemporary psychiatric medicine. In the past few decades, attempts have been made ​​​​​​to apply concepts adopted from complexity science to better understand complex human behavior. We propose that the complexity of mental illness can be studied under a general framework by quantifying the order and randomness of dynamic macroscopic human behavior and microscopic neuronal activity. Additionally, substantial effort is required to identify the link between macroscopic behaviors and microscopic changes in the neuronal dynamics within the brain.  

What is complexity?

Generally, complexity refers to a system with multiple components that are intricately entwined together, such as the subway network of the New York City. In the analogy of human physiology, such complexity can be viewed as numerous body components interacting at levels ranging from molecules, cells, to organs. Conventionally, scientists employ a reductionist approach to disassemble the system into constituent pieces, examine each component, and, finally, reassemble them, recreating the original entity. However, this approach is often unrealistic. In most circumstances, we can only observe the macroscopic output of physiological functions, such as an EEG, heart rate, and respiration, and mental functions, such as cognition, mood, and behavior. Even using the most sophisticated imaging techniques that employ functional magnetic resonance imaging (fMRI), a change in the intensity of a single brain voxel still represents compound responses from millions of neurons.   

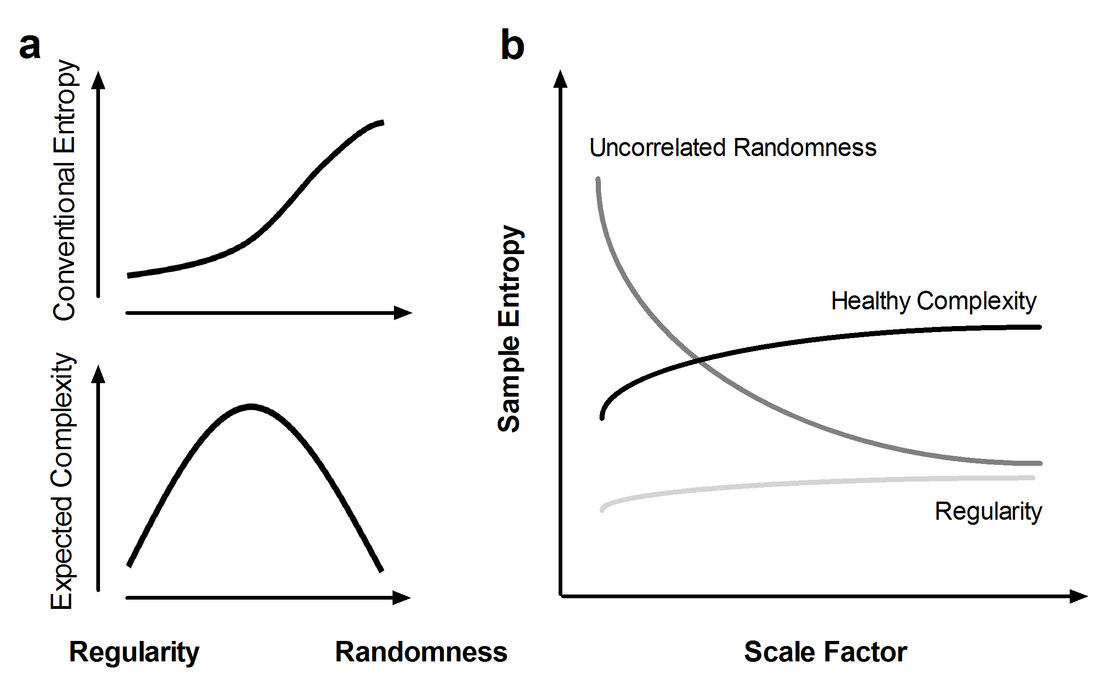
Therefore, a rea​​​​​​sonable method for measuring complexity is to observe a system's behavior in temporal time scales. A system may behave in either an ordered or random manner. However, the physical meaning of the randomness does not equal that of the complexity ( Goldberger et al ., 2002). The measurement of complexity should also incorporate the amount of information conveyed in the system. Differences in the physical meaning of randomness and complexity can be illustrated intuitively using texts as an example.
图片

A monkey typing produces random and incomprehensible text (A), whereas the unfortunate writer in the psychological horror movie   The  Shining  (1980) repeatedly typed the sentence “all work and no play makes Jack a dull boy” on reams of paper (C). The monkey typing represents a random process, and the unfortunate writer display compulsive and ordered behavior. Unlike Shakespeare's famous quote (B), both random and ordered conditions barely convey information that is rich enough to be “complex.” 

Multiscale entropy

A meaningful measure of complexity has been proposed by quantifying entropy over multiple time scales, also known as multiscale entropy (MSE) (Costa et al., 2002, 2005). The detail of MSE can be found at  http://www.physionet.org/physiotools/mse/ . A conceptual illustration of MSE is provided below. A conventional entropy method involves measuring irregularity and assigning a higher value when the irregularity of a given signal is increased. However, because conventional entropy is measured in the shortest time scale, the measured irregularity can represent either true complexity or merely uncorrelated randomness. Therefore, increased irregularity does not imply increased complexity (Goldberger, 1996; Goldberger, et al., 2002b). An ideal complexity measure assigns a high value to signals with a long-range correlation and other nonlinear properties (e.g., 1/f noise) and assigns a low value to signals with either regularity or uncorrelated randomness.
​
According to the theory that complex dynamics arise from multiple time scales and that a generic approach for measuring global complexity must consider multiple time scales in a given physical system (Fogedby, 1992; Zang, 1991), MSE analysis (Costa, et al., 2002; Costa, et al., 2005) was developed to estimate sample entropy in multiple time scales by using a coarse-graining procedure. Sample entropy is used in MSE analysis because it provides greater consistency and is less dependent on a given signal length compared with other entropy methods (Richman and Moorman, 2000). MSE calculation can be summarized in the following three steps: (a) constructing coarse-grained time series according to different scale factors; (b) quantifying the sample entropy of each coarse-grained time series; and (c) examining the sample entropy profile over a range of scales. According to this method, the length of each coarse-grained time series is equal to the length of the original time series divided by the scale factor. For Scale 1, the time series is merely the original time series. 
Picture
Yang AC*, Hong CJ, Liou YJ, Huang KL, Huang CC, Liu ME, Lo MT, Huang NE, Peng CK, Lin CP, Tsai SJ. Decreased resting-state brain activity complexity in schizophrenia characterized by both increased regularity and randomness. Human Brain Mapping 36(6):2174-86 (2015).

Multiscale entropy analysis of EEG signals

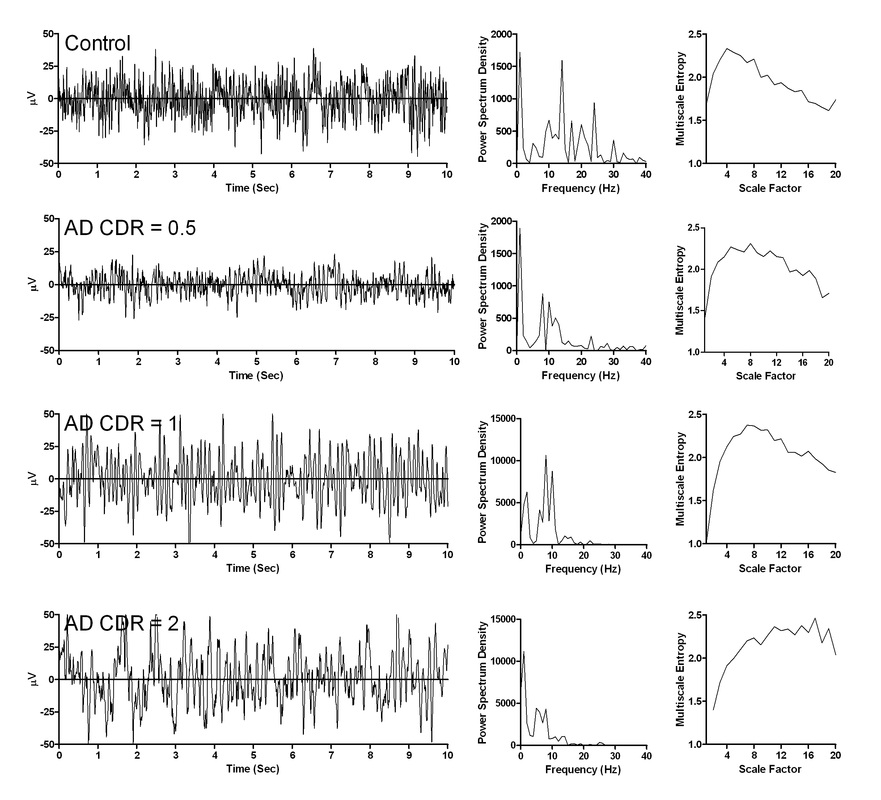
The original development of MSE was applied mainly to heart rate time series, with the parameters commonly being set as m = 2 and r = 0.15 (Cheng et al., 2009; Costa et al., 2002; Norris et al., 2008a; Yang et al., 2011). However, studies on EEG signals have examined the use of several other parameters, such as m = 1 and r = 0.25 (Escudero et al., 2006), m = 2 and r = 0.15 (Catarino et al., 2011), m = 2 and r = 0.20 (Mizuno et al., 2010; Takahashi et al., 2010; Takahashi et al., 2009), and m = 2 and r = 0.50 (Protzner et al. , 2011). We evaluated the use of MSE in EEG signals obtained from patients with Alzheimer's disease and found the parameters of m = 2 and r = 0.15 is appropriate in calculating MSE for EEG signals.
图片
Yang AC  , Wang SJ, Lai KL, Tsai CF, Yang CH, Hwang JP, Lo MT, Huang NE, Peng CK, Fuh JL*. Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer's disease. Progress in Psychopharmacology & Biological Psychiatry 47:52-61 (2013).

Multiscale entropy analysis of functional MRI BOLD signals

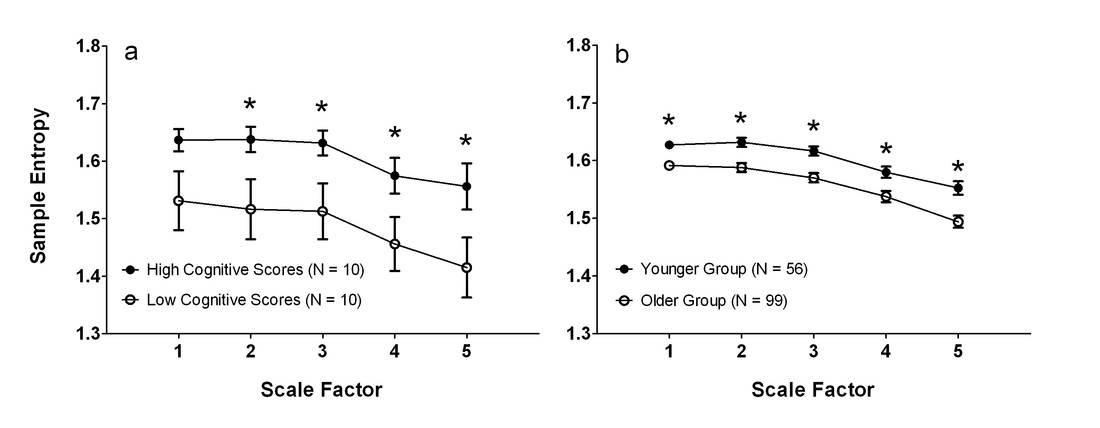
BOLD time series are usually short (100-200 time points), and the coarse-grained procedure in M​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​ SE with a large scale factor (over scale 5 ) may result in short data length and subsequently unreliable sample entropy estimation . To ameliorate this issue, we have estimated the appropriate parameters for MSE calculation from relatively short BOLD signals using parameters of m = 1; r = 0.35; and scale factor up to 5 [Yang et al . 2013 ].

For voxelwise analysis, a simplified approach can be taken to average the entropy value across all scale factors, and used this averaged entropy as the overall MSE value for a single BOLD time series. For individual resting fMRI data, MSE of BOLD signal can be computed at voxelwise levels in all cortical and subcortical gray matter voxels to create the whole-brain MSE parametric map for subsequent group analysis. MSE maps are spatially smoothed (FWHM = 8 mm) to minimize the differences in the functional anatomy of the brain across subjects.
图片

Decreased Resting-State Brain Activity Complexity in Schizophrenia Characterized by Both Increased Regularity and Randomness

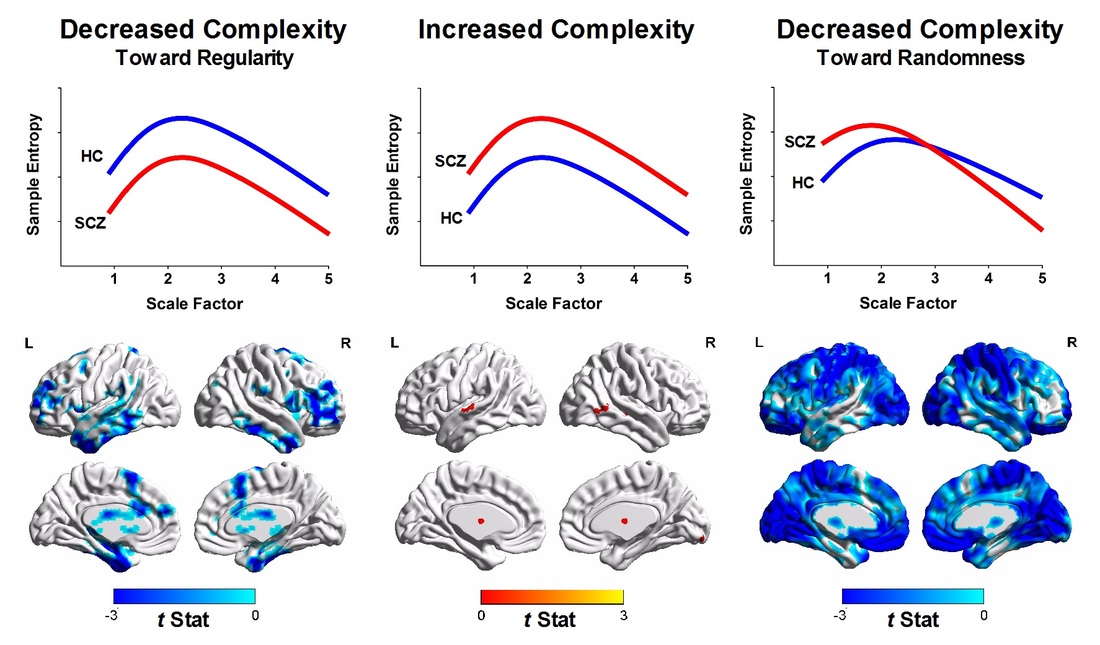
Schizophrenia is characterized by heterogeneous pathophysiology. Using multiscale entropy (MSE) analysis, which enables capturing complex dynamics of time series, we characterized MSE patterns of blood-oxygen-level-dependent (BOLD) signals across different time scales and determined whether BOLD activity in patients with schizophrenia exhibits increased complexity (increased entropy in all time scales), decreased complexity toward regularity (decreased entropy in all time scales), or decreased complexity toward uncorrelated randomness (high entropy in short time scales followed by decayed entropy as the time scale increases). We recruited 105 patients with schizophrenia with an age of onset between 18 and 35 years and 210 age- and sex-matched healthy volunteers. Results showed that MSE of BOLD signals in patients with schizophrenia exhibited two routes of decreased BOLD complexity toward either regular or random patterns. Reduced BOLD complexity toward regular patterns was observed in the cerebellum and temporal, middle, and superior frontal regions, and reduced BOLD complexity toward randomness was observed extensively in the inferior frontal, occipital, and postcentral cortices as well as in the insula and middle cingulum. Furthermore, we determined that the two types of complexity change were associated differently with psychopathology; specifically, the regular type of BOLD complexity change was associated with positive symptoms of schizophrenia, whereas the randomness type of BOLD complexity was associated with negative symptoms of the illness. These results collectively suggested that resting-state dynamics in schizophrenia exhibit two routes of pathologic change toward regular or random patterns, which contribute to the differences in syndrome domains of psychosis in patients with schizophrenia.
Picture
​Quantification of complexity changes in patients with schizophrenia (SCZ) relative to healthy controls (HC) according to MSE profiles. (Left) Brain regions with the regularity type of complexity changes of BOLD signals (i.e., decreased sample entropy over all scale factors in SCZ relative to HC). (Middle) Brain regions with increased complexity of BOLD signals (i.e., increased sample entropy over all scale factors in SCZ relative to HC). Color shown in brain mapping represents raw t-statistics of difference of MSE profile between SCZ and HC. No significant brain cluster was observed in this type of complexity change after correction for multiple comparisons. (Right) Brain regions with the randomness type of complexity change (i.e., increased sample entropy in short time scales followed by decay of sample entropy as the scale factor increases). 
Selected References

1. Yang AC, Tsai SJ*. Complexity of mental illness: A new research dimension. Progress in Neuro- Psychopharmacology & Biological Psychiatry 45:251-2 (2013). 

2. Yang AC*, Tsai SJ. Is mental illness complex? From behavior to brain. Progress in Neuro-Psychopharmacology & Biological Psychiatry 45:253 -7 (2013 ). 
​
3. Yang AC, Wang SJ, Lai KL, Tsai CF, Yang CH, Hwang JP, Lo MT, Huang NE, Peng CK, Fuh JL*. Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer's disease. Progress in Psychopharmacology & Biological Psychiatry 47:52-61 (2013).

4. Yang AC, Huang CC, Yeh HL, Liu ME, Hong CJ, Tu PC, Chen JF, Huang NE, Peng CK, Lin CP*, Tsai SJ*. Complexity of spontaneous BOLD activity in default mode network is correlated to cognitive Function in normal male elderly: a multiscale entropy analysis. Neurobiology of Aging 34(2):428-38 (2013). 

5. Yang AC, Huang CC, Liu ME, Liou YJ, Hong CJ, Lo MT, Huang NE, Peng CK, Lin CP, Tsai SJ*. The APOE ε4 allele affects complexity and functional connectivity of resting brain activity in healthy adults. Human Brain Mapping 35(7):3238-48 (2014).

6. Liang WK, Lo MT, Yang AC, Peng CK, Cheng SK, Tseng P, Juan CH. Revealing the brain's adaptability and the transcranial direct current stimulation facilitating effect in inhibitory control by multiscale entropy. Neuroimage 90; 218-34 (2014).

7. Wang CH, Tsai CL, Tseng P, Yang AC, Lo MT, Peng CK, Wang HY, Muggleton NG, Juan CH, Liang WK. The association of physical activity to neural adaptability during visuo-spatial processing in healthy elderly adults: A multiscale entropy analysis. Brain Cognition 29;92C:73-83 (2014).

8. Yang AC*, Hong CJ, Liou YJ, Huang KL, Huang CC, Liu ME, Lo MT, Huang NE, Peng CK, Lin CP, Tsai SJ. Decreased resting-state brain activity complexity in schizophrenia characterized by both increased regularity and randomness. Human Brain Mapping 36(6):2174-86 (2015).